デモンを用いた制約の定義

iZ-C では新しい制約を定義するためにデモンと呼ばれるインタフェースを提供しています。 制約伝播の際には CSint型変数の領域の変化を表わす幾つかのイベントが発生します。イベントは排他的な以下の4種類に分類されます。

Known:

領域は1つの値に縮小された (CSint型変数が即値化された場合です。)

Ex.: cs_EQ(vint, 0); /* Knownイベントが発生する例 */

NewMin:

領域の下限が変更された (必ず以前より大きな値に変化します。)

Ex.: cs_GT(vint, 0);

NewMax:

領域の上限が変更された (必ず以前より小さな値に変化します。)

Ex: cs_LT(vint, 0);

Neq:

領域から1つの値が取り除かれた

Ex: cs_NEQ(vint, 0);

これらのイベントが排他的であるとは、以下のことを意味します。

  • known イベント発生する場合には、newMin, newMax, neq イベントは発生しません。

  • newMinイベントおよびnewMaxイベントが発生する場合には、neq イベントは発生しません。

例えば、

CSint *vint = cs_createCSint(0, 10);
cs_GE(vint, 10);

の場合にはknown イベントが発生し(vint は10に即値化される)、newMin イベントは発生しません。

また、

CSint *vint = cs_createCSint(0, 10);
cs_NEQ(vint, 0);

の場合には、newMin イベントが発生し(vint は1より大きくなる)、neq イベントは発生しません。

例として、有名な N-クイーン の問題を cs_eventKnown() を使って記述してみましょう。

(8-クイーンは8つのクイーンをチェス盤上に、互いに取られないように垂直、 水平、対角線の位置を避けて配置するという問題です。)

クイーンの位置が決まったとき(すなわちCSint変数 allvars[i]でknownが発生したとき), 他のクイーンが同じ列および対角線上にないことを表現する必要があります。

#include <stdlib.h>
#include "iz.h"

// This function is called when allvars[index] is instantiated
// It returns FALSE if Constraints Propagation fails
IZBOOL knownQueen(int val, int index, CSint **allvars, int NbQueens, void *extra)
{
  int i;

  for (i = 0; i < NbQueens; i++) {
    if (i != index) {
      CSint *var = allvars[i];

      if (!cs_NEQ(var, val)) return FALSE;  // No queens on the same row
      if (!cs_NEQ(var, val + index - i)) return FALSE; //No queens on the same diagonal
      if (!cs_NEQ(var, val + i - index)) return FALSE;
    }
  }
  return TRUE;
}

int main(int argc, char **argv)
{
  int NbQueens = (argc > 1) ? atoi(argv[1]) : 8;
  CSint **allvars;

  cs_init();

  allvars = cs_createCSintArray(NbQueens, 1, NbQueens);

  cs_eventKnown(allvars, NbQueens, knownQueen, NULL);
  cs_search(allvars, NbQueens, cs_findFreeVarNbElementsMin);
  cs_printf("%A\n", allvars, NbQueens);

  cs_printStats();

  cs_end();

  return 0;
}

実行結果は以下のようになります。

1, 7, 4, 6, 8, 2, 5, 3

Nb Fails = 11
Nb Choice Points = 20
Heap Size = 1024

解である 1, 7, 4, 6, 8, 2, 5, 3 を図示すると以下のようになります。

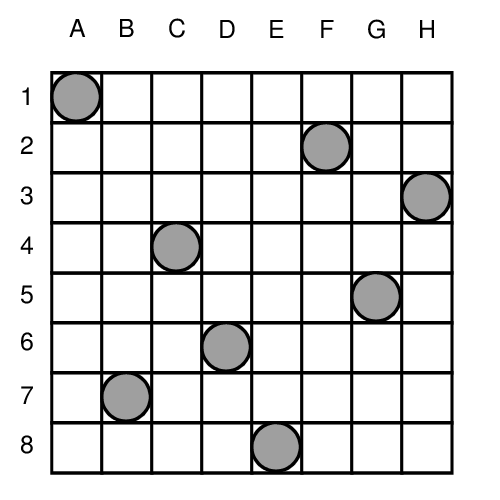
_images/queens-500x500.png

8-クイーンは92の解を持ちますがこれは

cs_findAll(allvars, NbQueens, cs_findFreeVarNbElementsMin, found)

を

cs_search(allvars, NbQueens, cs_findFreeVarNbElementsMin);

の代わりに使えば求められます。

found() は以下のように定義します。

void found(CSint **allvars, int NbQueens)
{
  static NbSolutions = 0;

  printf("Solution %d\n", ++NbSolutions);
  cs_printf("%A\n\n", allvars, NbQueens);
}

92 の解は289 回のバックトラックにより見つかります。55番目に求まる解は興味深いもので、 各行は5, 3, 1, 7, 2, 8, 6, 4 という列に配置されます。

_images/queens2-500x500.png